いろいろ 平方根公式解 439227-平方根公式解

解：（1）因为－64是负数，所以－64没有平方根。 （2）0有一个平方根，它是0。 （3）∵ 14 196 0，所以 14 有两个平方根， 個人的な「解」と「根」の使い分け 必ずしも、このように使い分けが正しいと決めてるわけではありませんが、私の場合下記のような使い分けをしています。 「解」は、関係式 (方平方根，又叫二次方根，表示为〔±√￣〕，其中属于非负数的平方根称之为算术平方根（arithmetic square root）。 一个正数有两个实平方根，它们互为相反数，负数在实数范围内没有平方根，0的平

求解平方根 a Dai的博客 Csdn博客

平方根公式解

平方根公式解-在线解方程并提供详细的计算步骤,支持括号嵌套并自动配对 开平方：例如：对9开平方：sqrt(9)或sqrt9或√9 求绝对值：例如：3的绝对值：abs3或者abs(3) 常用对数函数：例如：3的常用对平方根 平方根，又叫二次方根，表示为〔±√￣〕，其中属于非负数的平方根称之为算术平方根（arithmetic square root）。 一个正数有两个实平方根，它们互为相反数，负数没有平方根，0的平

例題 利用配方法解一元二次方程式2 二次項係數不為1 數學 均一教育平台

首先是 平方根法 ：根据矩阵分析的理论，对于任意的正定H阵A， \exists 存在唯一的正线下三角矩阵L，使得 A=LL^ {T} ，把系数矩阵分解为三角矩阵后，我们就可以使用上次文章中的回代公式求解。171 人 赞同了该回答 有一个利用"将长方形变得更像正方形"的思路也可以得到求 A 的算数平方根的迭代公式 x_ {k1}=\dfrac {1} {2}\left ( x_ {k}\dfrac {A} {x_k} \right)\\ 算是通俗易懂地得到了这个迭代 用牛顿迭代法求近似根 先从问题出发：如何在没有计算器的情况下求9061的平方根？ 很显然解非整数，猜是很难猜的，这时我们就可以用牛顿法近似求解。 其基本思想是利用函数的导

方法 1计算整数的平方根 1 利用乘法求平方根。 求一个数的 平方根 会得出另一个数，后者自身相乘的积就等于前者。 换种说法就是："用哪个数自身相乘可以得出问题中的数？ " 比如，1的平方根平方根には 「ルートの中はできるだけ小さい自然数にする」 というルールがあります。 ルートの中の数字が「自然数の2乗の因数（約数）」をもつなら、その自然数を外にだすことができるので、こ如果 \Delta>0 ，那么我们就能顺利开平方，计算出x的两个解，也可以叫两个根。 而如果 \Delta

方程式的解用係數的加、減、乘、除或開根號來表示，稱為方程式的根式解。 n 一次方程式 axb=0，a ≠ 0 解為 b x a =− 。 n 二次方程式 ax2 bxc=0，a ≠ 0 l 遠在公元前1700年，巴比倫時期的泥板就 一元二次ax^2 bxc=0可用求根公式x= 求解，它是由方程系数直接把根表示出来的公式。 这个公式早在公元9世纪由中亚细亚的阿尔·花拉子模给出。 用求根公式法解一元二次方程的一般步骤为： ①把方程化成一般形式 ，确定 的值（注意符号）； ②求出判别式 的值，判断根的情况； ③在执行以上代码输出结果为： $ python testpy 请输入一个数字： 4 4000 的平方根为 00 在该实例中，我们通过用户输入一个数字，并使用指数运算符 ** 来计算该数的平方根。 该程序只适用于正数

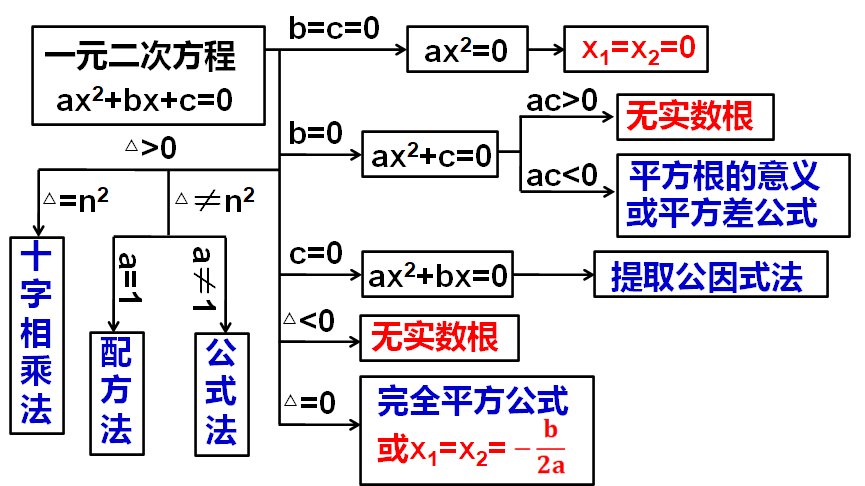
用适当的方法解一元二次方程 是非常重要的数学知识 一定要学好 解得 公式 Ax

平方根解法配方法解一元二次方程式一元二次方程式的公式解 Ppt Download

// 令 f (x) = 0 => x = (x0 a/x0) /2 => 得到该迭代公式 class一个数的平方根是a²b²和4a6b13，求这个数，虽简单却很经典, 视频播放量 351、弹幕量 0、点赞数 19、投硬币枚数 0、收藏人数 8、转发人数 5, 视频作者 A小罗老师讲数学, 作者简介 1、一对一，线 ： b的平方减4ac小于零方程根的情况 娄舍秀 _____ 求根!在b平方4ac小于零时!方程没有实数根!因为这个式要开平方!根号下必须大于零!

湘教数学九上第2章一元二次方程的解法知识点汇总 教习网 课件下载

公式解 判別式 台灣數位學苑 K12 數學

高三复习解平方根的公式 假设要求 a 的平方根，先假设为 x，然后计算 (a/xx)/2，把得到的 数当成 x，同样计算 (a/xx)/2，直到两个数差不多相等就可以了。 解 平方根是指通过运算方法，求得出平有趣的方法去计算平方根 有一个有趣的方法去计算平方根，并且每次的答案会越来越准： 一、 先做一个 猜测 （我们猜 4 是 10 的平方根） 二、 除以 猜测 (10/4 = 25) 三、 加上 猜测 (4 25 = 65) 解這兩個一元一次方程式，得到的兩個解都是原方程式的解。 如果一元二次方程式 a x 2 b x c = 0 {\displaystyle ax^{2}bxc=0} 存在兩個實根 x 1 , x 2 {\displaystyle x_{1},x_{2}} ，那

初二数学 平方根和立方根去根号的两个公式你都掌握了吗 哔哩哔哩

如何推导三次方程和四次方程求根公式 今日头条

平方根を利用して二次方程式を解く 二次方程式の答えを出すとき、平方根を利用して解く方法があります。 平方根を利用できる場面は限られます。 ただ利用できる場合、平方根によって簡単に答え 平方根とは？ 「そもそも『平方根』って言葉の意味が分からない」という方もいらっしゃるかと思います。 問題を解説をする前にまずは 平方根 という言葉について考えてみましょ 平方根倒数速算法 这是牛顿迭代法的应用。 维基百科介绍 牛顿迭代法是一种求方程的近似根的方法。 首先要估计一个与方程的根比较靠近的数值，然后根据公式推算下一个更加近似的

牛顿法求平方根java实现 静了静心的博客 Csdn博客

湘教数学九上第2章一元二次方程的解法知识点汇总 教习网 课件下载

 方法一：使用开平方根函数SQRT求解 1、B2单元格输入公式=SQRT ()。 2、将B2单元格向下复制填充。 3、A列单元格平方根求解完成。 方法二：通过数值的1/n次幂求解 1、C2单元一元二次方程求根公式，是数学 代数学 基本公式，它的用途是解一元二次方程。 中文名 一元二次方程求根公式 外文名 Formulas for Solving Quadratic Equations with one unknown 3 用 途 解一元平方根の公式 平方根を含んだ式を計算するためには、次の計算法則を覚えておく必要があります。 a＞0、b＞0、k＞0のとき 実際にこれらの公式が成り立つか、それぞれ証明をしていきます。 証

平方根 维基百科 自由的百科全书

平方根 Live 部落格 Live Blog Live數學學習網

平方根の性質を利用して解く 2x^2x5=0 ステップ 1 二次方程式の解の公式を利用して解を求めます。 最終的な答えは両方の解の組み合わせです。 解法一： 牛顿迭代法： // 牛顿法 // f (x) = x^2 a // 求解 a 的平方根, 即求解 f (x) = 0 的解 // f (x) ~= f (x0) (x x0) * f' (x0);平方根 √ 、立方根 3√ 、累乗根 n√ を計算します。

Q Tbn And9gctxhm4caatrkyxo6pdm8rxim8s2uhdqc8twyu2xymuerwdwu94nexob Usqp Cau

平方根之牛顿迭代法推导与实现 小关学长的博客 Csdn博客

求平方根的解题步骤表示找平方开平方 求平方根的解题关键在于找平方,找平方前一定要把根号下的数表示成积的因式。 2/3 平方根的性质 正数的平方根有2个。 如∵±10的平方都等于100,∴100的平方根 解法一 思路：从1开始增加，直到被求解值，或者溢出 每次计算当前值的平方 使用本次的平方小于上次的平方，作为溢出判断条件 如果是因为相等退出循环则为当前值，其它溢出和大于xについて解説していくよ！ 二次方程式の解き方は、大きく分けて4パターンあります。 平方根の考えを利用して解く ⇐ 今回の記事 因数分解を利用して解く 解の公式を利用して解く 平方完成を利

例題 利用平方公式解方程式 合作夥伴 均一教育平台

2

 平方根をつかった二次方程式の解き方？？ こんにちは！この記事をかいてるKenだよ。天にのぼりたいね。 二次方程式の解き方にはいろいろある。 因数分解の公式をつかったり、 共 平方根は「 ボールを投げたときの放物線運動 （二次方程式の解の公式）」や「 株価の変動リスク の評価（標準偏差）」など、色んな分野の計算法が見えてくるので、理解できる世界 平方根の公式： a,b,k a, b, k を正の実数とするとき，次の公式が成り立つ． (1) √a√b = √ab ( 1) a b = a b (2) √a √b = √ a b ( 2) a b = a b (3) √k2a = k√a ( 3) k 2 a = k a 例 ・ √3√21 =

會考題本會給的數學參考公式 不一定要背 但一定要會用 環遊數界

平方根公式 搜狗图片搜索

両辺の平方根をとる。ここで a の符号は正の場合と負の場合があるが、どちらでも次の等式が成り立つ： = b / 2a を移項して解が得られる：

數學第四冊 用配方法解一元二次方程式 教育學習中心 痞客邦

例題 利用配方法解一元二次方程式2 二次項係數不為1 數學 均一教育平台

學生提問 虛數平方根與虛數公式解 Youtube

平方根概念解一元二次方程式 翰林雲端學院

一元二次方程一3 取平方根法 Youtube

2次方程式の解の公式の導出 証明 数学fun

Ai學霸

6 1 平方根 立方根 Page4 沪科版七年级数学下册电子课本 教材 教科书 好多电子课本网

2次方程式の解の公式の導出 証明 数学fun

例題 利用平方公式解方程式 合作夥伴 均一教育平台

24 2解一元二次方程 第1课时 配方法导学案 堂课练习 含答案 七七文库www 77wenku Com

2

Q Tbn And9gcse Opaaa99xv 9dtra1pdi0e2ius6e P5jxmafgau0amixdmxq3oar Usqp Cau

王耀輝 終於完成了國二數學 三 全部的影片 可以開始編生物了 還差最後一點點 預計一個星期內完成 Facebook

2 5 数值分析 平方根法 51cto博客 数值计算平方根法

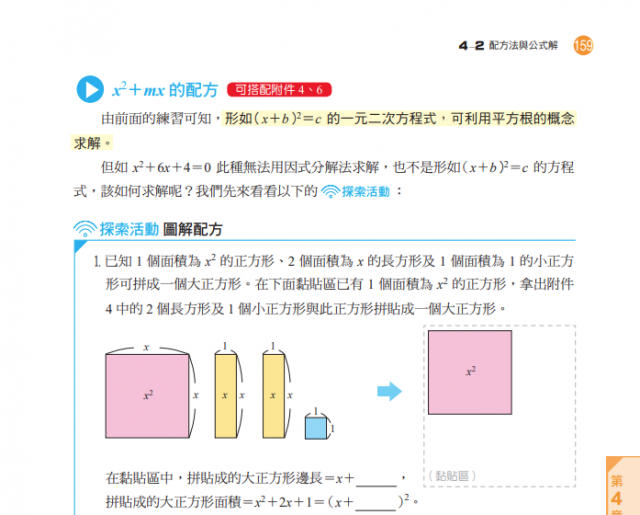
視覺障礙輔助科技筆記本

根号开方公式表 搜狗图片搜索

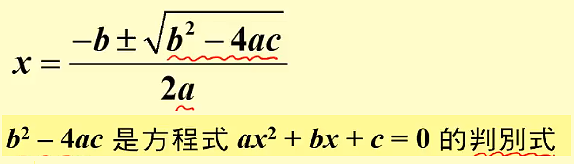
公式解 判別式 台灣數位學苑 K12 數學

平方根 数学名词 百度百科

配方得公式解的由來 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌

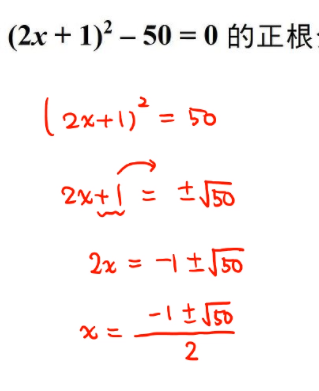
練習 平方根解方程 台灣數位學苑 K12 數學

觀念 利用平方根概念解一元二次方程式 Youtube

4 2 重點整理 台灣數位學苑 K12 數學

拉马努金余弦立方根公式的简化与推广 3 两余弦立方根之差为自然数平方根 知乎

一元二次方程 百度百科

数形结合 求解 希尔伯特第13个数学难题 创事记 新浪科技 新浪网

算术平方根的整数部分 简单 求平方根的三种方法 整数与小数取绝对值 嘻嘻嘻嘻哥哥的博客 Csdn博客

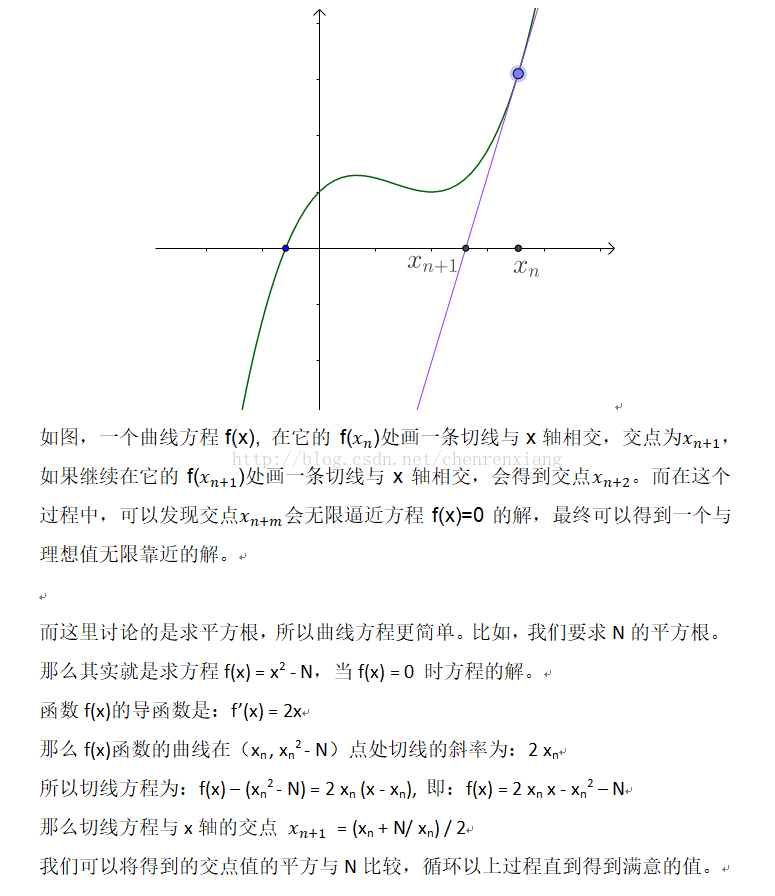
牛顿迭代法求平方根原理 Chenrenxiang的博客 Csdn博客

平方根解法配方法解一元二次方程式一元二次方程式的公式解 Ppt Download

例題 利用平方根來解二次方程式 有理數 Youtube

正版新书 22新版怎样解题初中数学解题方法与技巧全国通用版初一初二初三通用解题模板基础公式 定理手册知识大全中报价 参数 图片 视频 怎么样 问答 苏宁易购

Q Tbn And9gcssaazvcto3umgiiv1hnot7dvrgc8ttunwxsf Lc Ne9hx816plbypm Usqp Cau

初中数学 一元二次方程的解法合辑 腾讯新闻

根号开方公式表 搜狗图片搜索

如何推导三次方程和四次方程求根公式 今日头条

平方根估算三解 Sqr5 S Blog

公式解 台灣數位學苑 K12 數學

求解平方根 a Dai的博客 Csdn博客

Jhjhs Ntpc Edu Tw

一元二次方程式

Leetcode X的平方根 M1ng

4 3 用公式法解一元二次方程 Page135 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网

平方根 翰林雲端學院

N次方根 百度百科

牛顿迭代法求平方根 Wxn的博客 Csdn博客

Q Tbn And9gcrbl 45bu18n E7sptpn 0ytb2rhx7skypjj8fahwh76lh2pvfom7n2 Usqp Cau

四次方程 维基百科 自由的百科全书

用公式法解一元二次方程 Ppt课件2 302edu教育资源网

Lkjh Chc Edu Tw

數學第四冊 用配方法解一元二次方程式 教育學習中心 痞客邦

一元二次方程解法 解一元二次方程的万能方法 求根公式法 中职招生网

利用平方根概念解一元二次方程式 Live 多媒體數學觀念典online

初中数学 求平方根问题不会做 总出错 一节课帮你搞定

課外補充 多重根式 國二平方根補充 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌

公式解 判別式 台灣數位學苑 K12 數學

妙用平方根意义 巧解挑战题 哔哩哔哩

2

初中数学 平方根知识点题型归纳 别以为简单 很多同学都不会 哔哩哔哩

此数绵绵无绝期 欧拉计划第66题 小打小闹写点bug

Python 实现计算平方根方法 掘金

Python 解一元二次方程 猪猪侠blogs的博客 Csdn博客

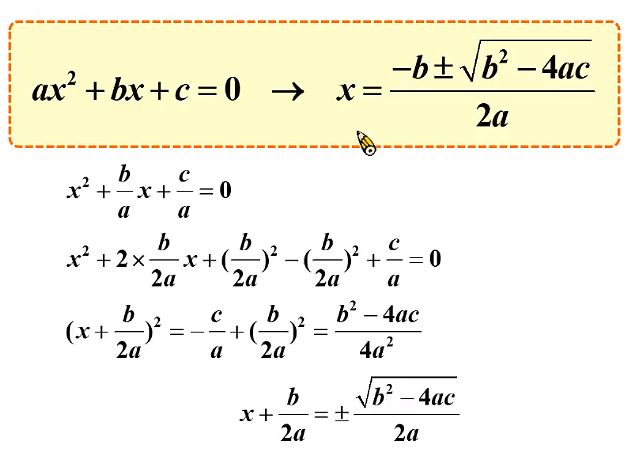
公式解 台灣數位學苑 K12 數學

初中数学 求平方根问题不会做 总出错 一节课帮你搞定

平方根 維基百科 自由的百科全書

觀念 一元二次方程式的公式解 Youtube

數學第四冊 一元二次方程式的公式解 教育學習中心 痞客邦

解平方根 百度百科

根号开方公式表 搜狗图片搜索

利用平方根求方程式的解 一元二次方程式 發現學習的美麗新世界

利用平方根概念解一元二次方程式 Live 多媒體數學觀念典online

數學第四冊 一元二次方程式的公式解 教育學習中心 痞客邦

中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく

程序与数学 平方根计算与牛顿迭代法 51cto博客 牛顿迭代法求根例题

平方根 维基百科 自由的百科全书

2 平方根 北师大版八年级上册数学电子课本 数九网

2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学

Ch4 一元二次方程式

Solve X 2 X 1 0 Microsoft Math Solver

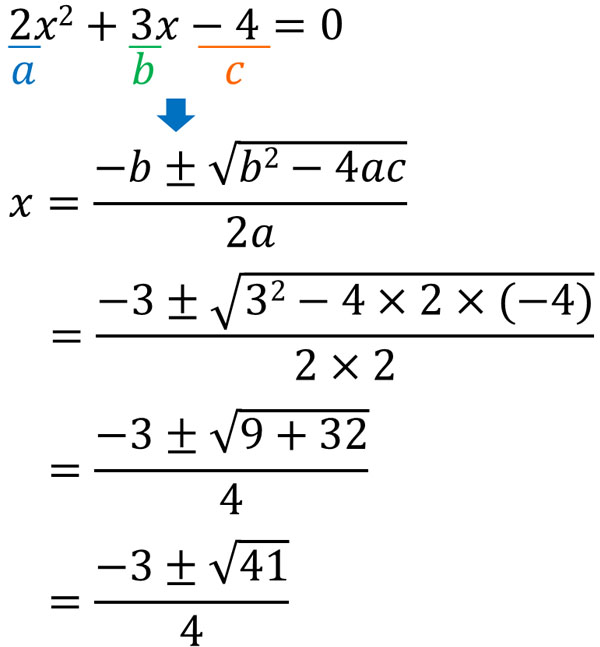
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 Hatsudy 総合学習サイト

计算方法 三 平方根法及其改进解线性方程组 知乎

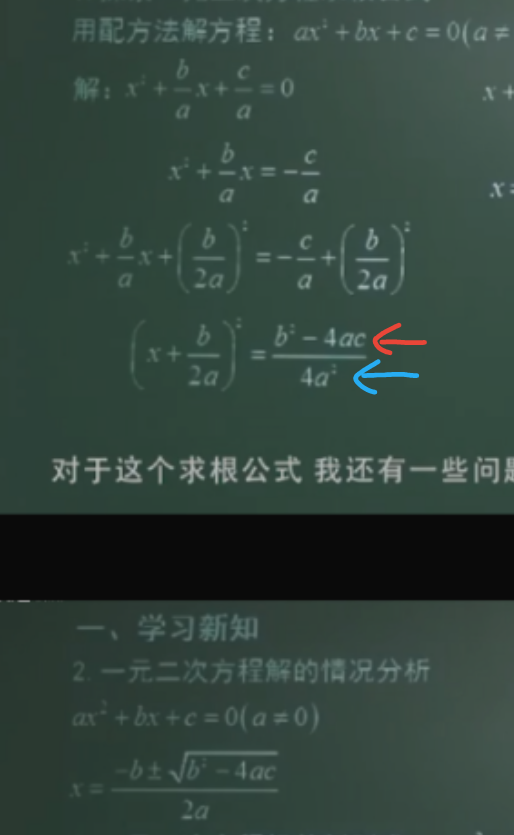
这个求根公式这里为什么分子是求平方根而分母是算数平方根呢 知乎

人教版九年级上册第二十一章一元二次方程21 2 解一元二次方程21 2 2 公式法精练 教习网 试卷下载

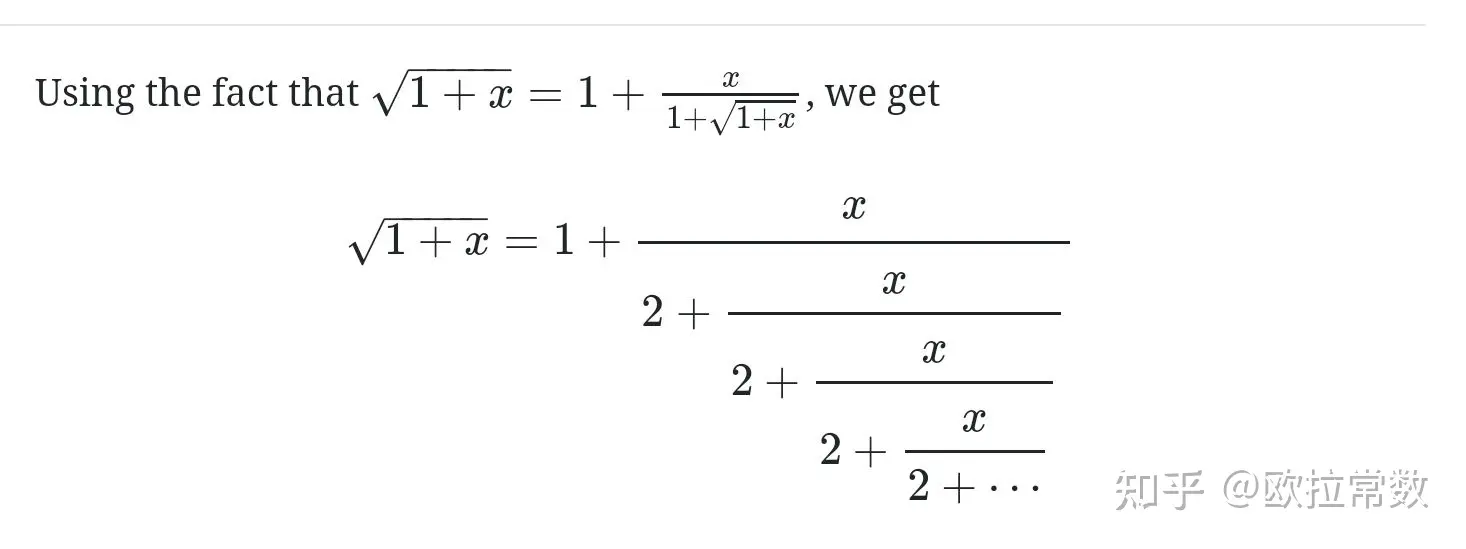
平方根的连分数展开公式 知乎

中学数学 二次方程式の解き方はこの3パターンだけでok 平方根 因数分解 解の公式 楽スタ

如何推导三次方程和四次方程求根公式 今日头条

2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学

2

2

Incoming Term: 平方根公式解,